TSegFormer: 3D Tooth Segmentation in Intraoral Scans with Geometry Guided Transformer
代码复现比较困难的地方是数据集的处理,因此下面主要介绍数据集处理的部分
个人使用的数据集
数据集需要有:三维点坐标以及点对应的标签
数据集处理
首先根据 data.py 和论文,我们可以得出数据集的格式:
feature,8 维向量,分别是 3 维点坐标+3 维法向量+高斯曲率+点”曲率”
label,标签,0-32,0 是牙龈
category,(1,0)为下颌骨,(0,1)为上颌骨
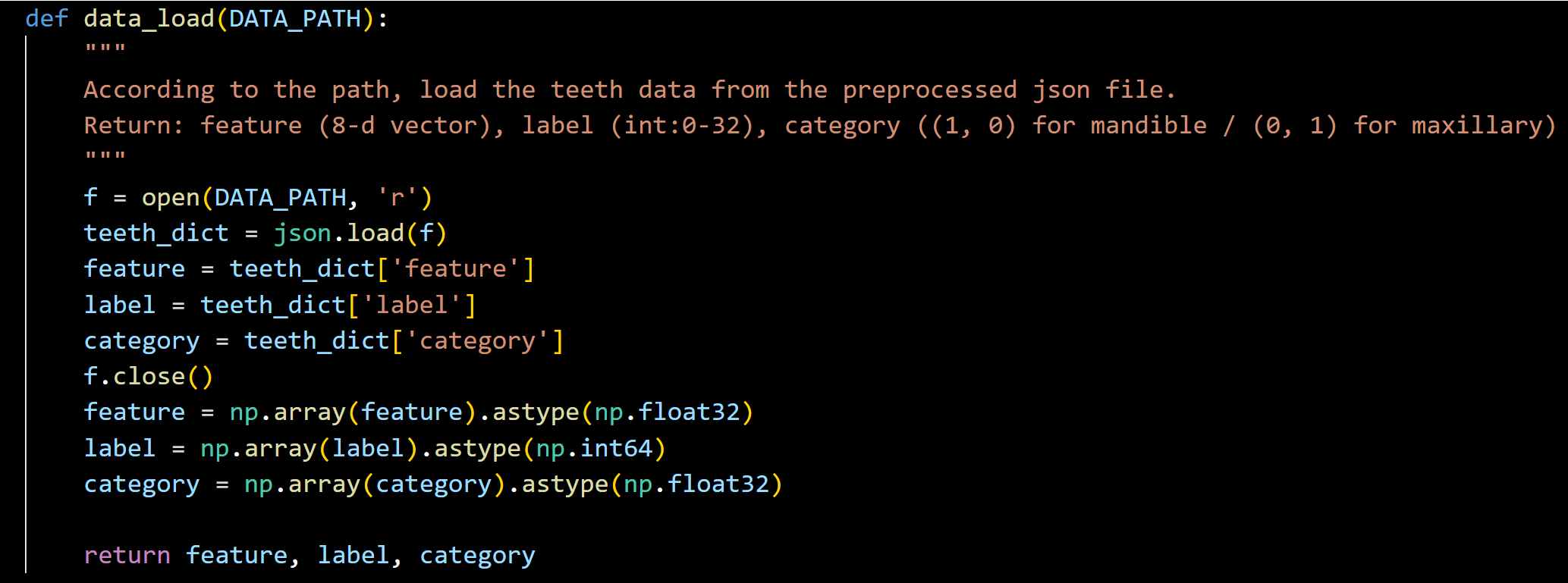
具体实现如下:
1.从.obj 文件中提取出点坐标
def read_obj_vertices(file_path):
vertices = []
with open(file_path, 'r') as file:
for line in file:
if line.startswith('v '): # 仅处理顶点行
parts = line.strip().split()
x, y, z = map(float, parts[1:4]) # 提取 x,y,z 坐标
vertices.append([x, y, z])
return np.array(vertices)2.计算法线,这里通过 open3d 计算
pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(vertex_array)
pcd.estimate_normals( search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=5.5, max_nn=30))
normals_array = np.asarray(pcd.normals)3.计算高斯曲率
Deepseek 生成的(不保证正确性),最后数据很大,所以在最后处理时,所有的数据进行了归一化处理
def compute_gaussian_curvature(points, normals, radius=0.1):
"""
计算点云中每个点的高斯曲率
参数:
points: numpy 数组,形状为(N, 3),表示点云中的点
normals: numpy 数组,形状为(N, 3),表示每个点的法向量
radius: 浮点数,用于确定邻域范围的半径
返回:
gaussian_curvatures: numpy 数组,形状为(N,),每个点的高斯曲率
"""
# 构建 KD 树以快速查找邻域点
tree = KDTree(points)
gaussian_curvatures = np.zeros(points.shape[0])
for i in range(points.shape[0]):
# 找到以当前点为中心,半径为 radius 的邻域内的点的索引
indices = tree.query_ball_point(points[i], radius)
neighborhood_points = points[indices]
# 如果邻域内点数不足,跳过
if len(neighborhood_points) < 3:
gaussian_curvatures[i] = 0
continue
# 计算协方差矩阵
mean_point = np.mean(neighborhood_points, axis=0)
centered_points = neighborhood_points - mean_point
cov_matrix = np.dot(centered_points.T, centered_points)
# 计算协方差矩阵的特征值
eigenvalues, _ = np.linalg.eig(cov_matrix)
eigenvalues = np.sort(eigenvalues)[::-1]
# 计算主曲率(这里简化处理,实际可能需要更复杂的曲面拟合)
k1 = eigenvalues[0]
k2 = eigenvalues[1]
# 高斯曲率是主曲率的乘积
gaussian_curvatures[i] = k1 * k2
return gaussian_curvatures4.计算点“曲率”
Deepseek 生成的(不保证正确性)
def compute_point_curvature_new(points, normals, radius=0.1):
"""
计算点云中每个点的新定义的点“曲率”
参数:
points (numpy.ndarray): 点云数据,形状为 (n_points, 3),其中 n_points 是点的数量
normals (numpy.ndarray): 点云的法向量,形状为 (n_points, 3)
radius (float): 邻域半径,默认为 0.1
返回:
numpy.ndarray: 每个点的曲率,形状为 (n_points,)
"""
n_points = points.shape[0]
curvatures = np.zeros(n_points)
# 使用 sklearn 的 NearestNeighbors 来查找每个点的邻域
nbrs = NearestNeighbors(radius=radius, algorithm='ball_tree').fit(points)
for i in range(n_points):
# 查找当前点的邻域点
distances, indices = nbrs.radius_neighbors([points[i]], return_distance=True)
neighbor_indices = indices[0]
if len(neighbor_indices) > 1:
# 获取当前点的法向量
current_normal = normals[i]
# 获取邻域点的法向量
neighbor_normals = normals[neighbor_indices]
# 计算当前点法向量与邻域点法向量的夹角余弦值
cos_angles = np.dot(neighbor_normals, current_normal)
# 计算曲率,这里定义为夹角余弦值的平均值
curvature = np.mean(cos_angles)
curvatures[i] = curvature
return curvatures 5.最终得到的数据进行归一化处理
def pc_normalize(pc):
centroid = np.mean(pc, axis=0)
pc = pc - centroid
m = np.max(np.sqrt(np.sum(pc ** 2, axis=1)))
pc = pc / m
return pc
vertices = pc_normalize(vertices)
normals = pc_normalize(normals)
gaussian_curvatures = gaussian_curvatures / 100000000006.labels 转换
def number_covert(original):
num_map = {
31:1,
32:2,
33:3,
34:4,
35:5,
36:6,
37:7,
38:8,
41:9,
42:10,
43:11,
44:12,
45:13,
46:14,
47:15,
48:16,
11:17,
12:18,
13:19,
14:20,
15:21,
16:22,
17:23,
18:24,
21:25,
22:26,
23:27,
24:28,
25:29,
26:30,
27:31,
28:32
}
new_list = [num_map.get(x, x) for x in original]
return new_list7.修改 data.py
def data_load(DATA_PATH):
"""
According to the path, load the teeth data from the preprocessed json file.
Return: feature (8-d vector), label (int:0-32), category ((1, 0) for mandible / (0, 1) for maxillary)
"""
f = open(DATA_PATH + ".json", 'r')
teeth_dict = json.load(f)
label = teeth_dict['labels']
f.close()
label = number_covert(label)
label = np.array(label).astype(np.int64)
# print(label)
cat = teeth_dict['jaw']
if cat == 'lower':
category = (1, 0)
else:
category = (0, 1)
category = np.array(category).astype(np.float32)
# print(category)
feature = np.concatenate((vertices, normals), axis=1)
feature = np.concatenate((feature, gaussian_array), axis=1)
feature = np.concatenate((feature, curvature_array), axis=1)
# print(feature)
return feature, label, category8.进行训练
python main.py --epochs 200 --num_points 10000